EPISTOLARY PURGATORY

I’ve come to depend a substantial amount on taking notes. This has supplemented my general creative tendencies around interpreting one thing in the context of something else. I have rigged-up a note taking system that spans many devices, SaaS tools and actual notebooks — one that is probably deserving of its own blog post.

However, all of that falls flat in one specific case: making a note of musical ideas. While I finally recognize the value of sheet music, it continues to be too elaborate a system for me to learn from scratch before I can use it without friction. A relatively flexible alternative to this is the Real-Book-style lead sheet, which contains minimalist representations of harmonies and melodies with a lot of room to interpret. I’d love a version of lead sheets that preserves the systems-style representation without relying on western music notation.

My work-in-progress solution to this comes from high-school chemistry: using Kekulé diagrams to represent scales. Kekulé structures are a minimalist method of representing aromatic organic compounds, where each bond is represented by a line or a dash, and carbon atoms are implied where two or more of these lines meet.

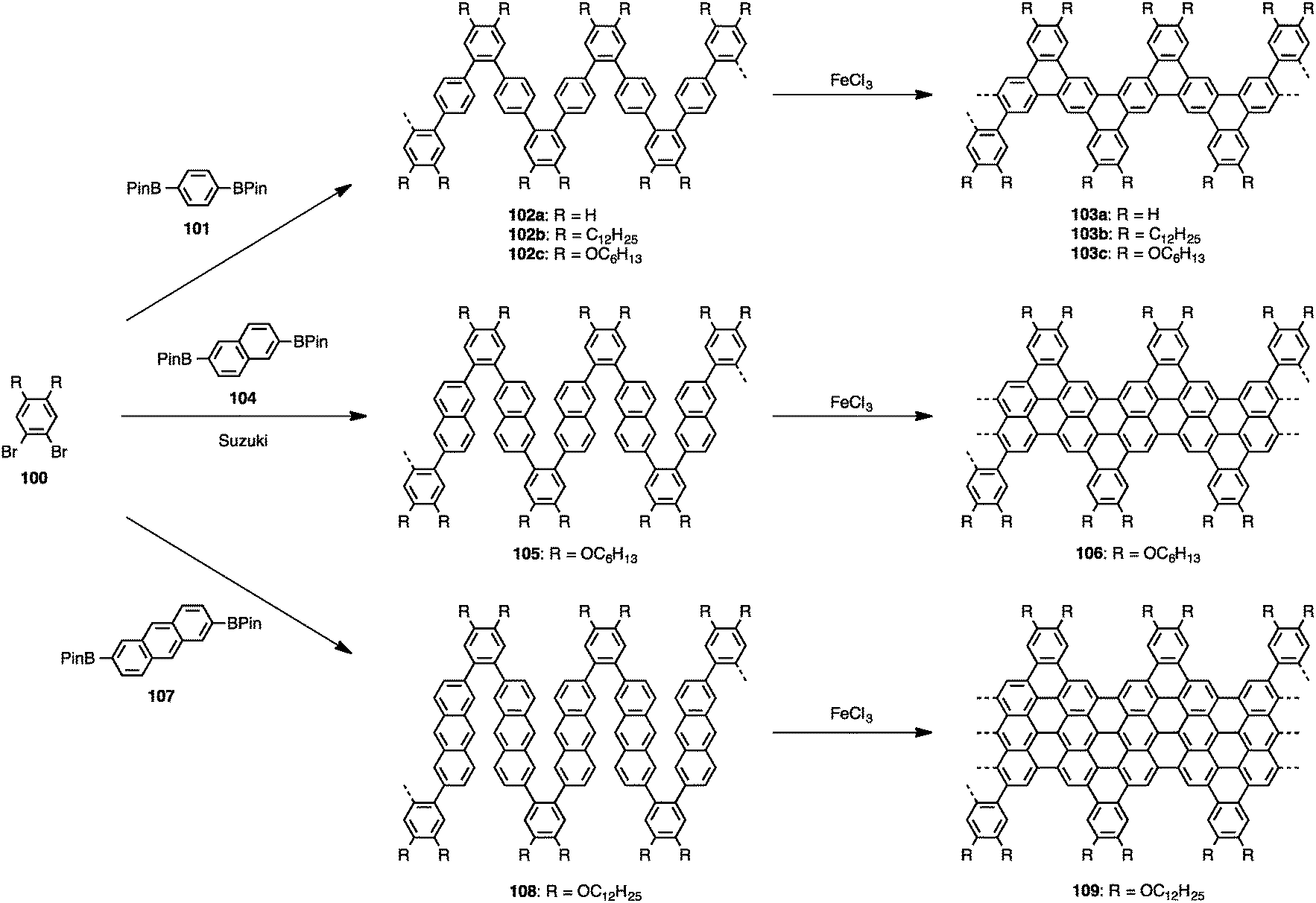
Kekulé diagrams in the study of Nanographenes (source: https://pubs.rsc.org/en/content/articlelanding/2015/cs/c5cs00183h)

In the context of music, the lines in Kekulé diagrams represent intervals, and vertices represent notes. Specifically, each line connecting two notes represents a half-step. In this way, a single bond would parallel with a half step interval, a double bond with whole step and so on. This style of notation assumes the circular nature of scales, reflecting the fact that we hear notes an octave apart as the same since they share a majority of the overtones.

Ethan Hein’s Pitch Wheel is an interesting concept built around the idea of circular representation of pitch classes, in which notes are along the circumference of a ring, each of which can be toggled on/off to build a scale. The pitch wheel makes a lot of sense in the context of music pedagogy, but has too many redundant parts. In a way, these Kekulé diagrams are a reduced version of the pitch wheel — one where the rings only contain scale degrees.

Representing a Musical Scale using the Kekulé structure

Step 1: Draw a regular polygon with the same number of sides as the number of notes in your scale. Let’s draw a major scale. A major scale has 7 notes, so the polygon will be a regular heptagon. Be sure to align your polygon such that there is an apex. This apex will be the root note.

Step 2: Starting from the top and moving clockwise, we denote every edge with a double line for whole step, and single line half steps. Our major scale diagram would hence have 5 whole steps and 2 half steps

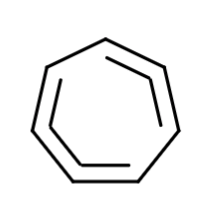
Major scale (WWHWWWH) represented as a Kekulé ring

Step 3: Label the apex with the root note of your scale. Let’s say in this case, C. The labelled apex, along with the interval lines, automatically implies what all the other notes are.

C major scale with the key and the implied notes

Symmetric scales can now be visualized in a way that makes symmetry very apparent.

Messiaen’s 1st, 2nd and 3rd Modes of Limited Transposition:

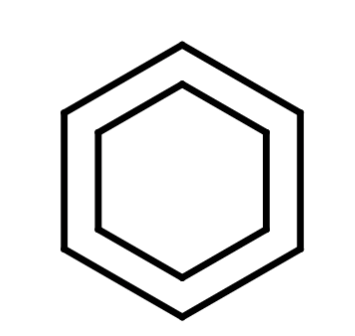
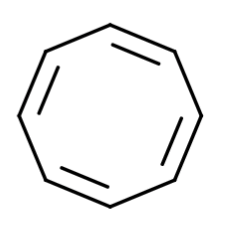
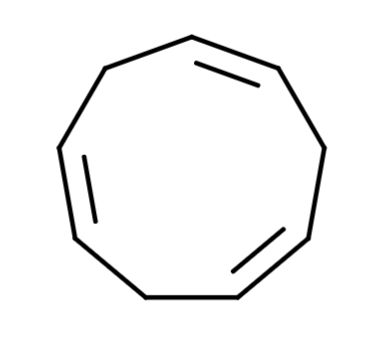
The exciting thing about this to me is the ability to visualize intervals and modes without fixating on individual notes or a key. I’ve been fascinated by this mode-first approach since discovering modal jazz, and am curious to what extent this method will allow me to quickly visualize my understanding in the context of free-improvisation on a mode.

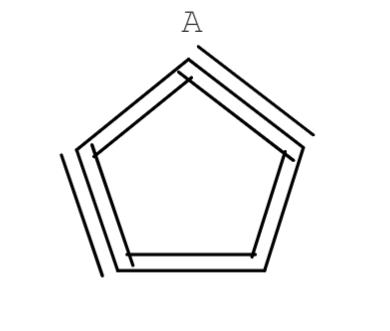
The A Minor pentatonic scale (Carbon atoms are fundamentally incapable of forming bonds like this)

The parallels between notation systems in music and organic chemistry are uncanny to say the least. It’s hard not to notice how similar the nomenclature of chords are to IUPAC nomenclature of organic compounds.

Kekulé diagrams allow for terse but informative representation of catenated aromatic compounds, which is probably why they have come to be widely adopted by organic chemists. Interestingly, Kekulé’s visualization technique also opened up study of new forms of isomorphism in aromatic compounds. I, too, foresee being able to use this method to analyse existing pieces of music.

I haven’t spent enough time with this system so obviously it leaves me with more questions than answers at the moment, some of which I would love to explore as I continue to use this:

• Are modes of a scale its isomers?
• How about visualizing modulation between two modes/scales using a system of two catenated rings with the pivot note or shared intervals?
• Is there a parallel between the transposition-invariance of scales and degeneracy?
• Can modal substitutions be visualized with some equivalent of a functional group?
• Can this system be twisted to work with xenharmonic tunings?
• Can the physical and chemical properties of scales be indulged in by studying organic compounds that they share a structure with?
• Conversely, can aromatic compounds be sonified and why is this idea trite?